结论
N维空间中点到超平面的距离为:
$$ d = \frac{\lvert \vec{w}^T \vec{x}+b\rvert}{\lvert\lvert w \rvert\rvert} $$
证明
前置证明
证明: $$w$$ 是 $$\vec{w}^T \vec{x} + b = 0$$ 这个平面的法向量。
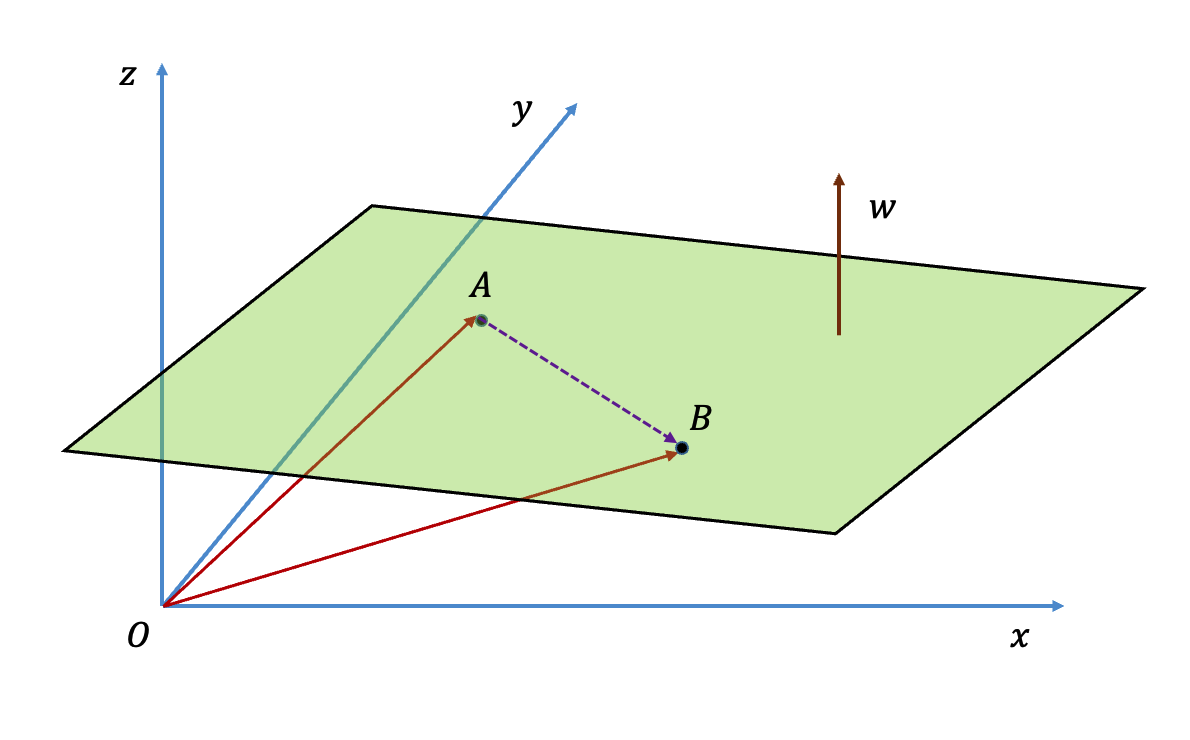
设 $$\vec{w}^T \vec{x} + b = 0$$ 张成的平面为 $$S$$, $$A$$、$$B$$ 为平面 $$S$$ 上的任意两点,则 $$\vec{OA}$$ 和 $$\vec{OB}$$ 为从原点指向 $$A$$、$$B$$ 两点的向量,因此 $$\vec{OA} - \vec{OB} = \vec{BA}$$ 为平面 $$S$$ 中的一个向量。由于 $$A$$ 和 $$B$$ 的任意性,$$\vec{BA}$$ 可以表示平面 $$S$$ 中的任意一个向量。
设 $$A$$ 和 $$B$$ 对应的点分别为 $$\vec{x}_1$$ 和 $$\vec{x}_2$$ ,有
$$ \begin{aligned} \vec{w}^T \vec{x}_1 + b &= 0 \ \vec{w}^T \vec{x}_2 + b &= 0 \ \end{aligned} $$
因此,
$$ \vec{w}^T (\vec{x}_1 - \vec{x}_2) = 0 $$
即,$$\vec{w}^T$$ 与平面 $$S$$ 内的任意向量 $$\vec{BA}$$ 的内积为 $$0$$ , 因此,$$\vec{w}$$ 是平面 $$S$$ 的法向量。
正式证明
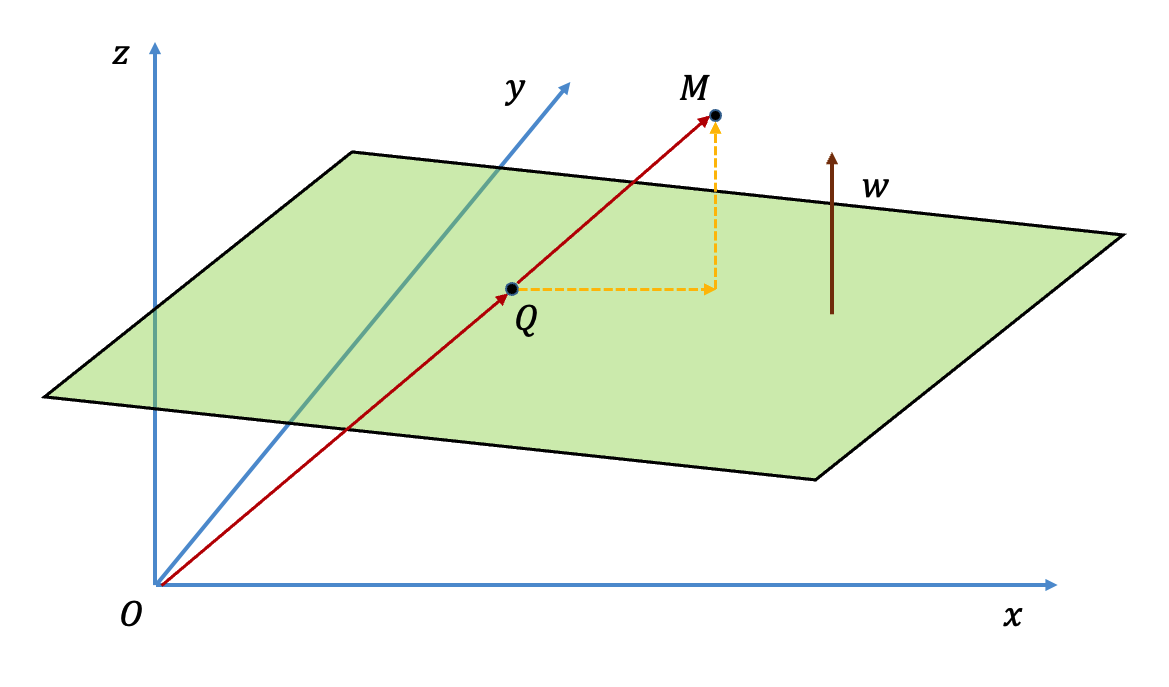
设 $$M$$ 为空间中任意一点,对应坐标为 $$\vec{x}$$ ,$$M$$ 到原点 $$O$$ 的连线与平面 $$S$$ 的交点为 $$Q$$,对应坐标为 $$\vec{y}$$,则 $$M$$ 到平面 $$S$$ 的距离 $$d$$,即为 $$\vec{QM}$$ 在法向量 $$\vec{w}$$ 上的投影长度。
$$ d = \frac{\lvert <\vec{w},\vec{QM}> \rvert}{\lvert\vert \vec{w} \rvert\rvert} $$
其中, $$\vec{QM} = \vec{OM} - \vec{OQ} = \vec{x} - \vec{y}$$ ,且 $$Q$$ 在平面 $$S$$ 中,因此,
$$ \begin{aligned} & \vec{w}^T \vec{y} + b = 0 \ & \vec{w}^T \vec{y} = -b \ \end{aligned} $$
又,
$$ \begin{aligned} \lvert <\vec{w},\vec{QM}> \rvert &= \lvert \vec{w}^T (\vec{x} - \vec{y}) \rvert \ \lvert <\vec{w},\vec{QM}> \rvert &= \lvert \vec{w}^T \vec{x} - \vec{w}^T \vec{y} \rvert \ \lvert <\vec{w},\vec{QM}> \rvert &= \lvert \vec{w}^T \vec{x} + b \rvert \end{aligned} $$
因此,点 $$M$$ 到平面 $$S$$ 的距离为,
$$ d = \frac{\lvert \vec{w}^T \vec{x} + b \rvert}{\lvert\lvert \vec{w} \rvert\rvert} $$